antony math 03

Sabtu, 14 Januari 2012

friend

Friend is a heart that has been clean doused the Divine Word
Companions is a noble soul who always prejudiced emotions and intentions lead promiscuously
Friends of the Love and Hate
Friend is quiet and flowering
Friends of the sorrow and cheerful ...
Friend is ... ..
Friend is something that understand the slightest mood
Friend who understands everything that is hidden
Friend is ... ... a guiding passion iniquity, who directs the disobedience of mind, which leads the desire greed, arrogance and pride which mamapah towards the Divine Way
Friends of the ... ... ... ... ... ... ... ... .. ... ... ... ... ..
"Ourselves who already know who we are"

arti sahabat

“Mempunyai satu sahabat sejati lebih berharga dari seribu teman yang mementingkan diri sendiri”

“Dalam masa kejayaan, teman-teman mengenal kita. Dalam kesengsaraan, kita mengenal teman-teman kita. Ingatlah kapan terakhir kali anda berada dalam kesulitan. Siapa yang berada di samping anda??. Siapa yang mengasihi anda saat anda merasa tidak dicintai??”

“Semua orang pasti membutuhkan sahabat sejati, namun tidak semua orang berhasil mendapatkannya. Banyak pula orang yang telah menikmati indahnya persahabatan, namun ada juga yang begitu hancur karena dikhianati sahabatnya”

“Proses dari teman menjadi sahabat membutuhkan usaha pemeliharaan dari kesetiaan, tetapi bukan pada saat kita membutuhkan bantuan barulah kita memiliki motivasi mencari perhatian, pertolongan dan pernyataaan kasih dari orang lain, tetapi justru ia berinisiatif memberikan dan mewujudkan apa yang dibutuhkan oleh sahabatnya”

“Seorang sahabat tidak akan menyembunyikan kesalahan untuk menghindari perselisihan, justru karena kasihnya ia memberanikan diri menegur apa adanya”

“Sahabat tidak pernah membungkus pukulan dengan ciuman, tetapi menyatakan apa yang amat menyakitkan dengan tujuan sahabatnya mau berubah”

“Persahabatan diwarnai dengan berbagai pengalaman suka dan duka, dihibur-disakiti, diperhatikan-dikecewakan, didengar-diabaikan, dibantu-ditolak, namun semua ini tidak pernah sengaja dilakukan dengan tujuan kebencian”

“Persahabatan tidak terjalin secara otomatis tetapi membutuhkan proses yang panjang seperti besi menajamkan besi, demikianlah sahabat menajamkan sahabatnya”

Selasa, 15 November 2011

matriks invers

Mencoba memenuhi permintaan dari sobat Bryan untuk posting tentang invers dan determinan matriks, maka pada postingan kali ini akan mencoba membahas sedikit materi yang berkaitan dengan invers dan determinan matriks.

Matriks merupakan susunan bilangan-bilangan berbentuk persegi atau persegi panjang yang diatur menurut baris dan kolom tertentu. Matriks dinotasikan dengan huruf kapital. Jika m adalah banyaknya baris dari matriks $A$ , dan n adalah banyaknya kolom dari matriks $A$ , maka matriks $A$ mempunyai ordo $m \times n$ , atau ditulis $A_{m\times n}$ .

$A_{m \times n} = \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n}\\ \vdots & \vdots & \cdots &\vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{bmatrix}$

1. Invers Matriks

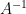Jika A dan B adalah matriks persegi, dan berlaku $A \cdot B = B \cdot A = I$ maka dikatakan matriks A dan B saling invers. B disebut invers dari A, atau ditulis $A^{-1}$ . Matriks yang mempunyai invers disebut invertible atau matriks non singular, sedangkan matriks yang tidak mempunyai invers disebut matriks singular.

Untuk mencari invers matriks persegi berordo 2×2, coba perhatikan berikut ini.
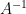Jika $A = \begin{bmatrix} a & b \\ c & d \end{bmatrix}$ dengan $ad - bc \neq 0$ , maka invers dari matriks A (ditulis $A^{-1}$ ) adalah sebagai berikut:

$A^{-1} = \frac {1}{ad - bc} \begin{bmatrix} d & -b \\ -c & a \end{bmatrix}$

Jika $ad - bc = 0$ maka matriks tersebut tidak mempunyai invers, atau disebut matriks singular.

Sifat-sifat matriks persegi yang mempunyai invers:

- $(A \cdot B)^{-1} = B^{-1} \cdot A^{-1}$
- $(B \cdot A)^{-1} = A^{-1} \cdot B^{-1}$
- $(A^{-1})^t =(A^{t})^{-1}$
Contoh: Tentukan invers dari matriks berikut!
$\begin {array} {lcl} A & = & \begin{bmatrix} 2 & 5 \\ 1 & 3 \end{bmatrix} \\ A^{-1} & = & \frac {1}{2 \times 3 - 1 \times 5} \begin{bmatrix} 3 & -5 \\ -1 & 2 \end{bmatrix} \\ & = & \frac {1}{6-5} \begin{bmatrix} 3 & -5 \\ -1 & 2 \end{bmatrix} \\ & = & \frac {1}{1} \begin{bmatrix} 3 & -5 \\ -1 & 2 \end{bmatrix} \\ A^{-1} & = & \begin{bmatrix} 3 & -5 \\ -1 & 2 \end{bmatrix}\end{array}$

2. Determinan Matriks

Syarat suatu matriks dapat dicari determinannya adalah matriks tersebut harus merupakan matriks persegi. Jika $A = \begin{bmatrix} a & b \\ c & d \end{bmatrix}$ , maka rumus untuk mencari determinan matriks berordo 2×2:

$det A = \begin{vmatrix} A \end{vmatrix} = \begin{vmatrix} a & b \\ c & d \end{vmatrix} = ad - bc$

Sedangkan untuk mencari determinan matriks berordo 3×3 menggunakan aturan Sarrus.

$A_{3 \times 3} = \begin{bmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{2n}\\ a_{31} & a_{32} & a_{33} \end{bmatrix}$

$\begin{vmatrix} A \end{vmatrix} = \begin{vmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{2n}\\ a_{31} & a_{32} & a_{33} \end{vmatrix} \begin{matrix} a_{11} & a_{12} \\ a_{21} & a_{22} \\ a_{31} & a_{32} \end{matrix}$

$\begin{array} {lcl} \begin{vmatrix} A \end{vmatrix} = && a_{11}a_{22}a_{33} + a_{12}a_{23}a_{31} + a_{13}a_{21}a_{32} \\ & - & a_{13}a_{22}a_{31} - a_{11}a_{23}a_{32} - a_{12}a_{21}a_{33} \end{array}$

Contoh: Tentukan determinan dari matriks berikut!

$A = \begin{bmatrix} 3 & 1 \\ 5 & 2 \end{bmatrix}$

$\begin{vmatrix} A \end{vmatrix} = \begin{vmatrix} 3 & 1 \\ 5 & 2 \end{vmatrix} = 3 \times 2 - 1 \times 5 = 6 - 5 = 1$

$B = \begin{bmatrix} 1 & 2 & 3 \\ 1 & 3 & 4\\ 1 & 4 & 3 \end{bmatrix}$

$\begin{vmatrix} B \end{vmatrix} = \begin{vmatrix}1 & 2 & 3 \\ 1 & 3 & 4\\ 1 & 4 & 3 \end{vmatrix} \begin{matrix} 1 & 2\\ 1 & 3 \\ 1 & 4 \end{matrix}$

$\begin{array} {lcl} \begin{vmatrix} B \end{vmatrix} & = & 1.3.3 + 2.4.1 + 3.1.4 - 1.3.3 - 4.4.1 - 3.1.2 \\ & = & 9 + 8 + 12 - 9 - 16 - 6 \\ & = & -2 \end{array}$

PELUANG

1) Permutasi
Permutasi adalah susunan unsur-unsur yang berbeda dalam urutan tertentu. Pada permutasi urutan diperhatikan sehingga

Permutasi k unsur dari n unsur

adalah semua urutan yang berbeda yang mungkin dari k unsur yang diambil dari n unsur yang berbeda. Banyak permutasi k unsur dari n unsur ditulis

atau

.
Permutasi siklis (melingkar) dari n unsur adalah (n-1) !
Cara cepat mengerjakan soal permutasi

dengan penulisan nPk, hitung 10P4
kita langsung tulis 4 angka dari 10 mundur, yaitu 10.9.8.7
jadi 10P4 = 10x9x8x7 berapa itu? hitung sendiri :)

Contoh permutasi siklis :

Suatu keluarga yang terdiri atas 6 orang duduk mengelilingi sebuah meja makan yang berbentuk lingkaran. Berapa banyak cara agar mereka dapat duduk mengelilingi meja makan dengan cara yang berbeda?
Jawab :
Banyaknya cara agar 6 orang dapat duduk mengelilingi meja makan dengan urutan yang berbeda sama dengan banyak permutasi siklis (melingkar) 6 unsur yaitu :

2) Kombinasi
Kombinasi adalah susunan unsur-unsur dengan tidak memperhatikan urutannya. Pada kombinasi AB = BA. Dari suatu himpunan dengan n unsur dapat disusun himpunan bagiannya dengan untuk

Setiap himpunan bagian dengan k unsur dari himpunan dengan unsur n disebut kombinasi k unsur dari n yang dilambangkan dengan ,

Contoh :
Diketahui himpunan

.
Tentukan banyak himpunan bagian dari himpunan A yang memiliki 2 unsur!
Jawab :

Banyak himpunan bagian dari A yang memiliki 2 unsur adalah C (6, 2).

Cara cepat mengerjakan soal kombinasi

dengan penulisan nCk, hitung 10C4

kita langsung tulis 4 angka dari 10 mundur lalu dibagi 4!, yaitu 10.9.8.7 dibagi 4.3.2.1
jadi 10C4 = 10x9x8x7 / 4x3x2x1 berapa itu? hitung sendiri :)

Ohya jika ditanya 10C6 maka sama dengan 10C4, ingat 10C6=10C4. contoh lainnya
20C5=20C15
3C2=3C1
100C97=100C3
melihat polanya? hehe semoga bermanfaat!

Peluang Matematika

1. Pengertian Ruang Sampel dan Kejadian
Himpunan S dari semua kejadian atau peristiwa yang mungkin mucul dari suatu percobaan disebut ruang sampel. Kejadian khusus atau suatu unsur dari S disebut titik sampel atau sampel. Suatu kejadian A adalah suatu himpunan bagian dari ruang sampel S.

Contoh:
Diberikan percobaan pelemparan 3 mata uang logam sekaligus 1 kali, yang masing-masing memiliki sisi angka ( A ) dan gambar ( G ). Jika P adalah kejadian muncul dua angka, tentukan S, P (kejadian)!
Jawab :
S = { AAA, AAG, AGA, GAA, GAG, AGG, GGA, GGG}
P = {AAG, AGA, GAA}

2. Pengertian Peluang Suatu Kejadian
Pada suatu percobaan terdapat n hasil yang mungkin dan masing-masing berkesempatan sama untuk muncul. Jika dari hasil percobaan ini terdapat k hasil yang merupakan kejadian A, maka peluang kejadian A ditulis P ( A ) ditentukan dengan rumus :

Contoh :
Pada percobaan pelemparan sebuah dadu, tentukanlah peluang percobaan kejadian muncul bilangan genap!
Jawab : S = { 1, 2, 3, 4, 5, 6} maka n ( S ) = 6
Misalkan A adalah kejadian muncul bilangan genap, maka:
A = {2, 4, 6} dan n ( A ) = 3

3. Kisaran Nilai Peluang Matematika
Misalkan A adalah sebarang kejadian pada ruang sampel S dengan n ( S ) = n, n ( A ) = k dan

Jadi, peluang suatu kejadian terletak pada interval tertutup [0,1]. Suatu kejadian yang peluangnya nol dinamakan kejadian mustahil dan kejadian yang peluangnya 1 dinamakan kejadian pasti.

4. Frekuensi Harapan Suatu Kejadian
Jika A adalah suatu kejadian pada frekuensi ruang sampel S dengan peluang P ( A ), maka frekuensi harapan kejadian A dari n kali percobaan adalah n x P( A ).

Contoh :
Bila sebuah dadu dilempar 720 kali, berapakah frekuensi harapan dari munculnya mata dadu 1? Jawab :
Pada pelemparan dadu 1 kali, S = { 1, 2, 3, 4, 5, 6 } maka n (S) = 6.
Misalkan A adalah kejadian munculnya mata dadu 1, maka:
A = { 1 } dan n ( A ) sehingga :

Frekuensi harapan munculnya mata dadu 1 adalah

5. Peluang Komplemen Suatu Kejadian
Misalkan S adalah ruang sampel dengan n ( S ) = n, A adalah kejadian pada ruang sampel S, dengan n ( A ) = k dan Ac adalah komplemen kejadian A, maka nilai n (Ac) = n – k, sehingga :

Jadi, jika peluang hasil dari suatu percobaan adalah P, maka peluang hasil itu tidak terjadi adalah (1 – P).

Peluang Kejadian Majemuk

1. Gabungan Dua Kejadian
Untuk setiap kejadian A dan B berlaku :

Catatan :

dibaca “ Kejadian A atau B dan

dibaca “Kejadian A dan B”

Contoh :
Pada pelemparan sebuah dadu, A adalah kejadian munculnya bilangan komposit dan B adalah kejadian muncul bilangan genap. Carilah peluang kejadian A atau B!
Jawab :

2. Kejadian-kejadian Saling Lepas
Untuk setiap kejadian berlaku

Jika

. Sehingga

Dalam kasus ini, A dan B disebut dua kejadian saling lepas.

3. Kejadian Bersyarat
Jika P (B) adalah peluang kejadian B, maka P (A|B) didefinisikan sebagai peluang kejadian A dengan syarat B telah terjadi. Jika

adalah peluang terjadinya A dan B, maka

Dalam kasus ini, dua kejadian tersebut tidak saling bebas.

4. Teorema Bayes
Teorema Bayes(1720 – 1763) mengemukakan hubungan antara P (A|B) dengan P ( B|A ) dalam teorema berikut ini :

5. Kejadian saling bebas Stokhastik
(i) Misalkan A dan B adalah kejadian – kejadian pada ruang sampel S, A dan B disebut dua kejadian saling bebas stokhastik apabila kemunculan salah satu tidak dipengaruhi kemunculan yang lainnya atau : P (A | B) = P (A), sehingga:

Sebaran Peluang

1. Pengertian Peubah acak dan Sebaran Peluang.
Peubah acak X adalah fungsi dari suatu sampel S ke bilangan real R. Jika X adalah peubah acak pada ruang sampel S denga X (S) merupakan himpunan berhingga, peubah acak X dinamakan peubah acak diskrit. Jika Y adalah peubah acak pada ruang sampel S dengan Y(S) merupakan interval, peubah acak Y disebut peubah acak kontinu. Jika X adalah fungsi dari sampel S ke himpunan bilangan real R, untuk setiap

dan setiap

maka:

Misalkan X adalah peubah acak diskrit pada ruang sampel S, fungsi masa peluang disingkat sebaran peluang dari X adalah fungsi f dari R yang ditentukan dengan rumus berikut :

2. Sebaran Binom
Sebaran Binom atau Distribusi Binomial dinyatakan dengan rumus sebagai berikut :

Dengan P sebagai parameter dan

Rumus ini dinyatakan sebagai:

untuk n = 0, 1, 2, .... ,n
Dengan P sebagai parameter dan

P = Peluang sukses
n = Banyak percobaan
x = Muncul sukses
n-x = Muncul gaga